Preprints

2025

1. 

   Minimum reflux calculation for multicomponent distillation in multi-feed, multi-product columns: Algorithms and examples

   Zheyu Jiang, Mohit Tawarmalani, and Rakesh Agrawal

   2025

   Abs Bib HTML PDF

   In this work, we present the first algorithm for identifying the minimum reboiler vapor duty requirement for a general multi-feed, multi-product (MFMP) distillation column separating ideal multicomponent mixtures. This algorithm incorporates our latest advancement in developing the first shortcut model for MFMP columns. We demonstrate the accuracy and efficiency of this algorithm through case studies. The results obtained from these case studies also provide valuable insights on optimal design of MFMP columns. Many of these insights are against the existing design guidelines and heuristics. For example, placing a colder saturated feed stream above a hotter saturated feed stream sometimes leads to higher energy requirement. Furthermore, decomposing a general MFMP column into individual simple columns may lead to incorrect estimation of the minimum reflux ratio for the MFMP column. Thus, the algorithm presented here offers a fast, accurate, and automated approach to synthesize new, energy-efficient, and cost-effective MFMP columns.

   @misc{jiang2024mfmp2,
     title = {Minimum reflux calculation for multicomponent distillation in multi-feed, multi-product columns: Algorithms and examples},
     author = {Jiang, Zheyu and Tawarmalani, Mohit and Agrawal, Rakesh},
     year = {2025},
     eprint = {2503.20917},
     archiveprefix = {arXiv},
     doi = {https://doi.org/10.48550/arXiv.2503.20917},
   }

2. 

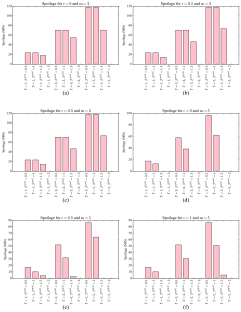   Joint Optimization of Fair Facility Allocation and Robust Inventory Management for Perishable Consumer Products

   Saba Ghasemi Naraghi, and Zheyu Jiang

   2025

   Abs Bib PDF

   Perishable consumer products like food, cosmetics, and household chemicals face challenges in supply chain management due to limited shelf life and uncertainties in demand and transportation. To address some of these issues, this work proposes a robust optimization framework for jointly optimizing facility allocation and inventory management. The framework determines optimal loca-tions for distribution centers and their assigned customers, as well as inventory policies that min-imize the total costs related to transportation, distribution, and storage under uncertain demand in a robust setting. Specifically, we develop a two-stage mixed-integer linear programming (MILP) model is that incorporates First-In-First-Out (FIFO) inventory policy to reduce spoilage. The bilinear FIFO constraints are linearized to improve computational efficiency. Social equity is integrated by defining a fairness index and incorporating it in facility allocation. Demand uncertainty is tackled using a robust optimization approach with affine demand functions to handle multiple scenarios. The model is solved using row and column generation techniques for scalability. Overall, this ro-bust optimization framework is expected to enhance supply chain resilience, reduce waste, and improve cost-effectiveness in managing perishable products.

   @misc{escape2025inventory,
     title = {Joint Optimization of Fair Facility Allocation and Robust Inventory Management for Perishable Consumer Products},
     author = {Ghasemi Naraghi, Saba and Jiang, Zheyu},
     year = {2025},
   }

3. 

   Multi-objective Optimization of Steam Cracking Microgrid for Clean Olefins Production

   Saba Ghasemi Naraghi, and Zheyu Jiang

   2025

   Abs Bib PDF

   Olefins are essential precursors in producing a wide range of chemical products, including plastics, detergents, adhesives, rubber, and food packaging. Ethylene and propylene are the most ubiquitous olefin components and are predominantly produced through steam cracking. However, steam cracking is highly energy- and carbon-intensive, making its decarbonization a priority as the energy sector shifts toward clean, renewable electricity. Electrifying the steam cracking process is a promising pathway to reduce carbon emissions. However, this is chal-lenged by the intrinsic conflict between the continuous operational nature of ethylene plants and the intermit-tent nature of renewable energy sources (e.g., solar and wind) in modern power systems. Massive energy storage systems or full plant reconfigurations to meet the power demand of electrified crackers are shown to be eco-nomically and practically infeasible. Thus, a more viable solution is to pursue a gradual electrification pathway and operate an ethylene plant as a microgrid that adopts diverse energy sources. To optimize the operational strategy of such a microgrid considering uncertainties in renewable energy generation and market prices, in this work, we introduce a stochastic multi-objective optimization approach that minimizes operating costs and car-bon emissions of steam cracking. Results from a case study not only elucidate the trade-offs between economic and environmental objectives, but also provide insights into the optimal operating scheme in sustainable eth-ylene production.

   @misc{escape2025microgrid,
     title = {Multi-objective Optimization of Steam Cracking Microgrid for Clean Olefins Production},
     author = {Ghasemi Naraghi, Saba and Jiang, Zheyu},
     year = {2025},
   }

4. 

   A Novel Bayesian Framework for Inverse Problems in Precision Agriculture

   Zeyuan Song, and Zheyu Jiang

   2025

   Abs Bib PDF

   An essential problem in precision agriculture is to accurately model and predict root-zone (top 1 m of soil) soil moisture profile given soil properties and precipitation and evapotranspiration information. This is typically achieved by solving agro-hydrological models. Nowadays, most of these models are based on the standard Rich-ards equation (RE), a highly nonlinear, degenerate elliptic-parabolic partial differential equation that describes ir-rigation, precipitation, evapotranspiration, runoff, and drainage through soils. Recently, the standard RE has been generalized to time-fractional RE with any fractional order between 0 and 2. Such generalization allows the characterization of anomalous soil exhibiting non-Boltzmann behavior due to the presence of preferential flow. In this work, we focus on inverse modeling of time-fractional RE; that is, how to accurately estimate the fractional order and soil property parameters of the fractional RE given soil moisture content measurements. Specifically, we introduce a novel Bayesian variational autoencoder (BVAE) framework that synergistically integrates our in-house developed fractional RE solver and adaptive Fourier decomposition (AFD) to accurately estimate the pa-rameters of time-fractional RE. Our proposed AFD-enhanced BVAE framework consists of a probabilistic encod-er, latent-to-kernel neural networks and convolutional neural networks. The BVAE framework is theoretically ex-plainable and enhanced by the AFD theory, a novel signal processing technique that achieves superior computa-tionally efficiency. Through illustrative examples, we demonstrate the efficiency and reliability of our AFD-enhanced BVAE framework.

   @misc{escape2025inverse,
     title = {A Novel Bayesian Framework for Inverse Problems in Precision Agriculture},
     author = {Song, Zeyuan and Jiang, Zheyu},
     year = {2025},
   }

5. 

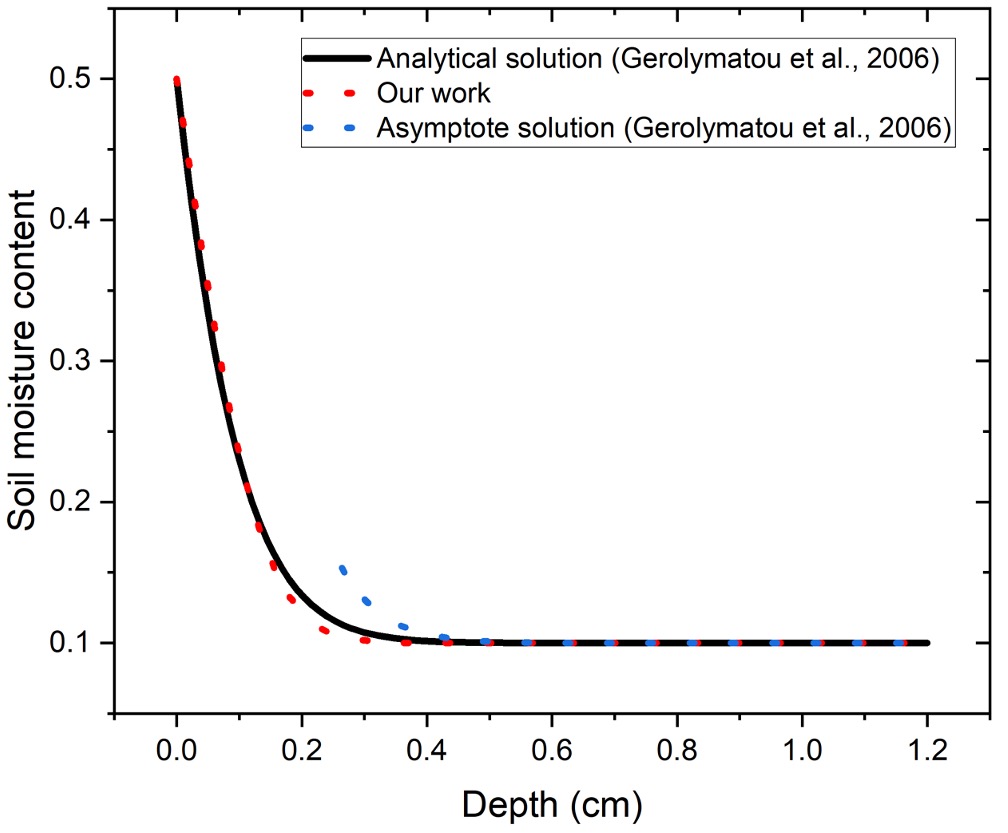   A Physics-based, Data-driven Numerical Framework for Anomalous Diffusion of Water in Soil

   Zeyuan Song, and Zheyu Jiang

   2025

   Abs Bib PDF

   Precision modeling and forecasting of soil moisture are essential for implementing smart irrigation systems and mitigating agricultural drought. Most agro-hydrological models are based on the standard Richards equation, a highly nonlinear, degenerate elliptic-parabolic partial differential equation (PDE) with first order time derivative. However, research has shown that standard Richards equation is unable to model preferential flow in soil with fractal structure. In such a scenario, the soil exhibits anomalous non-Boltzmann scaling behavior. Incorporating the anomalous non-Boltzmann scaling behavior into the Richards equation leads to a generalized, time-fractional Richards equation based on fractional time derivatives. As expected, solving the time-fractional Rich-ards equation for accurate modeling of water flow dynamics in soil faces extensive computational challenges. To target these challenges, we propose a novel numerical method that integrates finite volume method (FVM), adap-tive fixed point iteration scheme, and neural network to solve the time-fractional Richards equation. Specifically, we develop an adaptive fixed point iteration scheme to solve the FVM-discretized equation iteratively, which avoids the stability issues when directly solving a stiff and sparse matrix equation. To improve the solution quali-ty which is influenced by numerical errors and computational constraints during actual implementation, we pro-pose to use neural networks that resemble an encoder-decoder architecture to map soil moisture profiles into a latent space and reconstruct them back. Through 1-D examples, we illustrate the accuracy and computational ef-ficiency of our proposed physics-based, data-driven numerical method. Finally, we present a Markov chain Mon-te Carlo (MCMC) approach to solve the inverse problem to obtain soil-specific parameters given soil moisture solutions.

   @misc{escape2025fractional,
     title = {A Physics-based, Data-driven Numerical Framework for Anomalous Diffusion of Water in Soil},
     author = {Song, Zeyuan and Jiang, Zheyu},
     year = {2025},
   }

6. 

   Decarbonization of Steam Cracking for Clean Olefins Production: Optimal Microgrid Scheduling

   Saba Ghasemi Naraghi, Tylee Kareck, Lingyun Xiao, and 3 more authors

   2025

   Bib PDF

   @misc{saba2025bookchapter,
     title = {Decarbonization of Steam Cracking for Clean Olefins Production: Optimal Microgrid Scheduling},
     author = {Ghasemi Naraghi, Saba and Kareck, Tylee and Xiao, Lingyun and Reed, Richard and Ramanan, Paritosh and Jiang, Zheyu},
     year = {2025},
   }

7. 

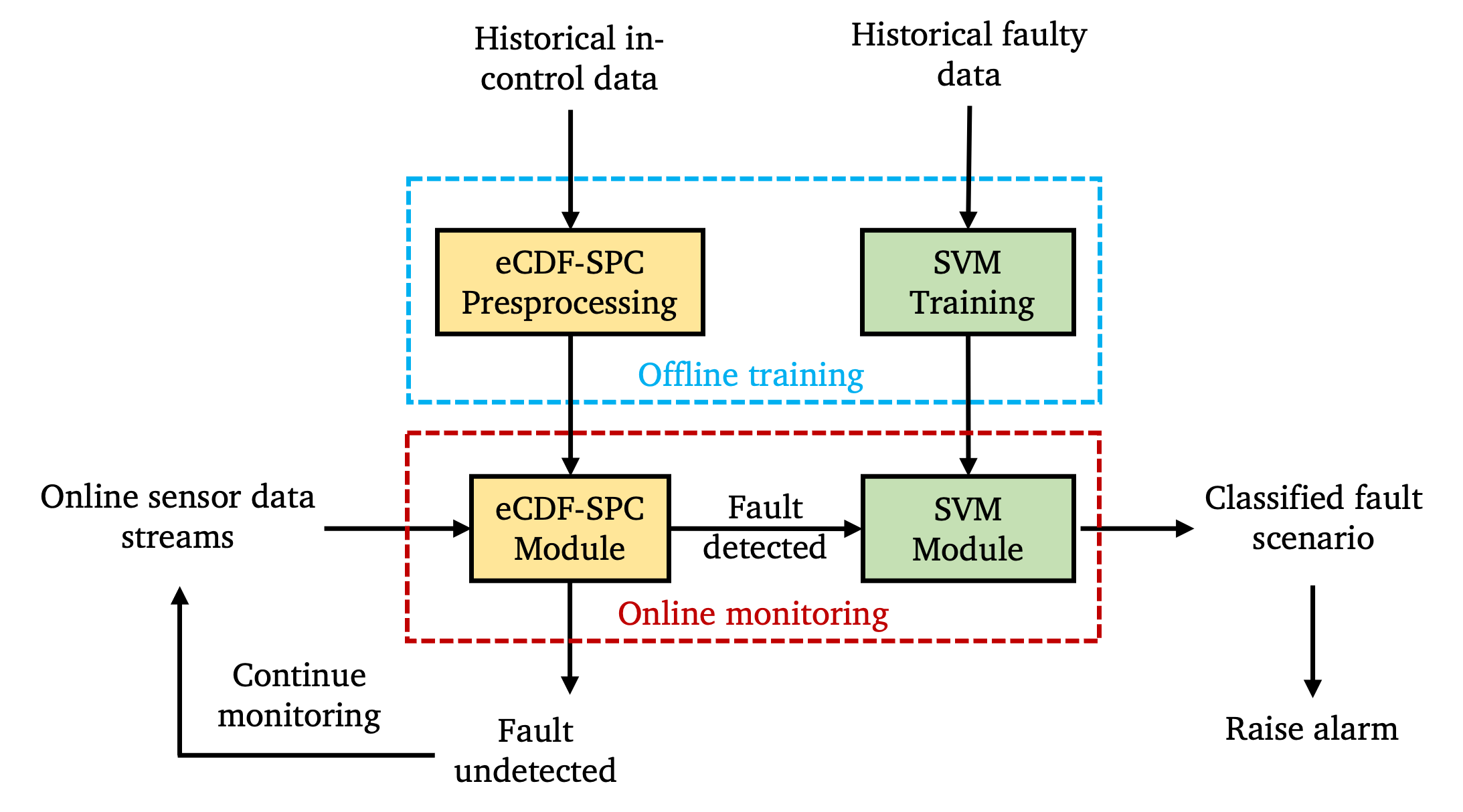   Online Fault Detection and Classification of Chemical Process Systems Leveraging Statistical Process Control and Riemannian Geometric Analysis

   Alireza Miraliakbar, Fangyuan Ma, and Zheyu Jiang

   2025

   Abs Bib HTML PDF

   In this work, we study an integrated fault detection and classification framework called FARM for fast, accurate, and robust online chemical process monitoring. The FARM framework integrates the latest advancements in statistical process control (SPC) for monitoring nonparametric and heterogeneous data streams with novel data analysis approaches based on Riemannian geometry together in a hierarchical framework for online process monitoring. We conduct a systematic evaluation of the FARM monitoring framework using the Tennessee Eastman Process (TEP) dataset. Results show that FARM performs competitively against state-of-the-art process monitoring algorithms by achieving a good balance among fault detection rate (FDR), fault detection speed (FDS), and false alarm rate (FAR). Specifically, FARM achieved an average FDR of 96.97% while also outperforming benchmark methods in successfully detecting hard-to-detect faults that are previously known, including Faults 3, 9 and 15, with FDRs being 97.08%, 96.30% and 95.99%, respectively. In terms of FAR, our FARM framework allows practitioners to customize their choice of FAR, thereby offering great flexibility. Moreover, we report a significant improvement in average fault classification accuracy during online monitoring from 61% to 82% when leveraging Riemannian geometric analysis, and further to 84.5% when incorporating additional features from SPC. This illustrates the synergistic effect of integrating fault detection and classification in a holistic, hierarchical monitoring framework.

   @misc{alirezaFOCAPDpaper,
     title = {Online Fault Detection and Classification of Chemical Process Systems Leveraging Statistical Process Control and Riemannian Geometric Analysis},
     author = {Miraliakbar, Alireza and Ma, Fangyuan and Jiang, Zheyu},
     year = {2025},
     eprint = {2504.01276},
     archiveprefix = {arXiv},
     doi = {https://doi.org/10.48550/arXiv.2504.01276},
   }

2024

1. 

   Physics-constrained Active Learning for Soil Moisture Estimation and Optimal Sensor Placement

   Jianxin Xie, Bing Yao, and Zheyu Jiang

   2024

   Abs Bib HTML PDF

   Soil moisture is a crucial hydrological state variable that has significant importance to the global environment and agriculture. Precise monitoring of soil moisture in crop fields is critical to reducing agricultural drought and improving crop yield. In-situ soil moisture sensors, which are buried at pre-determined depths and distributed across the field, are promising solutions for monitoring soil moisture. However, high-density sensor deployment is neither economically feasible nor practical. Thus, to achieve a higher spatial resolution of soil moisture dynamics using a limited number of sensors, we integrate a physics-based agro-hydrological model based on Richards equation in a physics-constrained deep learning framework to accurately predict soil moisture dynamics in the soil’s root zone. This approach ensures that soil moisture estimates align well with sensor observations while obeying physical laws at the same time. Furthermore, to strategically identify the locations for sensor placement, we introduce a novel active learning framework that combines space-filling design and physics residual-based sampling to maximize data acquisition potential with limited sensors. Our numerical results demonstrate that integrating Physics-constrained Deep Learning (P-DL) with an active learning strategy within a unified framework–named the Physics-constrained Active Learning (P-DAL) framework - significantly improves the predictive accuracy and effectiveness of field-scale soil moisture monitoring using in-situ sensors.

   @misc{jianxin2024pdl,
     title = {Physics-constrained Active Learning for Soil Moisture Estimation and Optimal Sensor Placement},
     author = {Xie, Jianxin and Yao, Bing and Jiang, Zheyu},
     year = {2024},
     eprint = {2403.07228},
     archiveprefix = {arXiv},
     primaryclass = {eess.SP},
     doi = {https://doi.org/10.48550/arXiv.2403.07228},
   }

2023

1. 

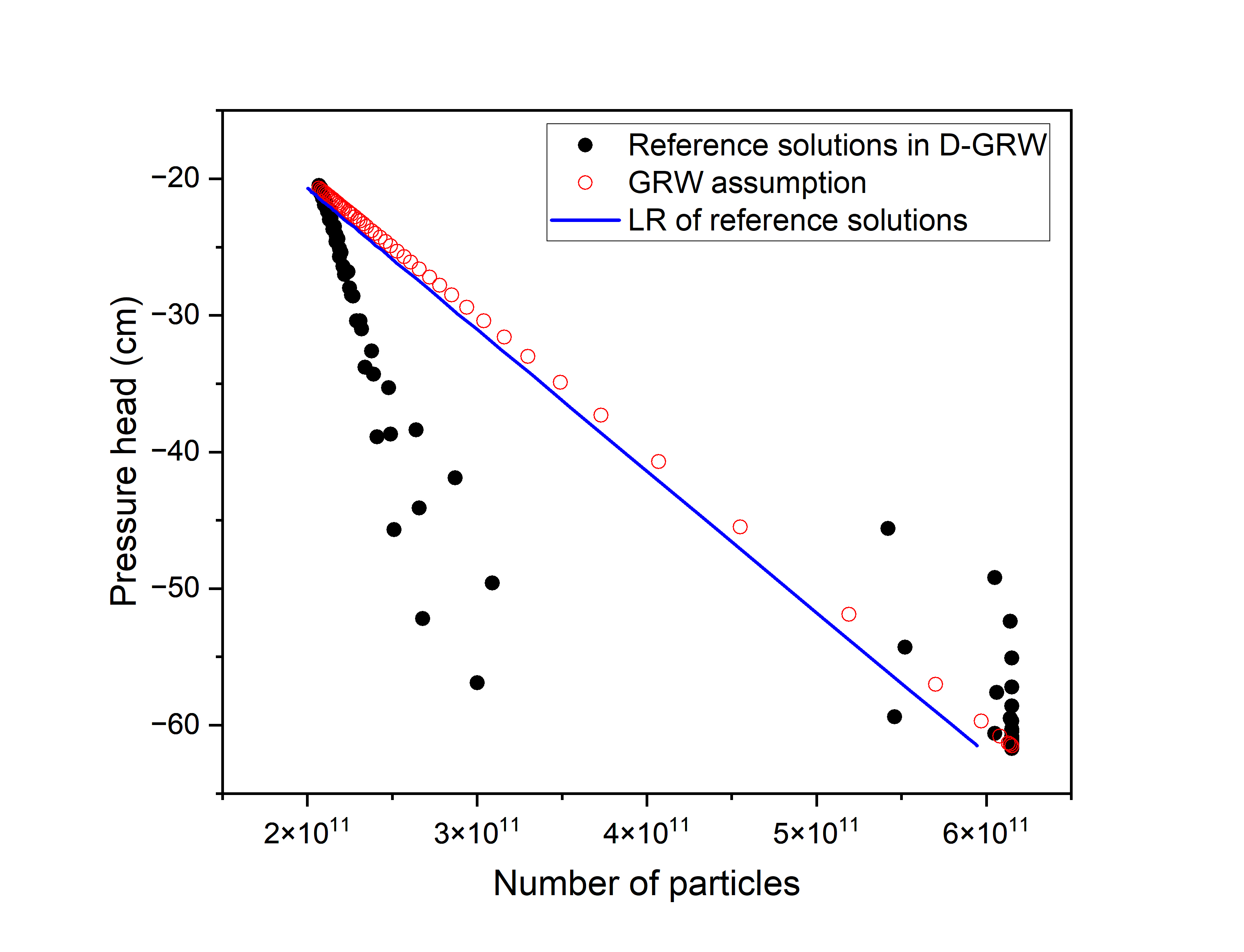   A Novel Numerical Method for Agro-Hydrological Modeling of Water Infiltration in Soil

   Zeyuan Song, and Zheyu Jiang

   2023

   Abs Bib PDF

   Root-zone soil moisture monitoring is essential for sensor-based precision agriculture, smart irrigation, and agricultural drought prevention. Modeling the spatiotemporal water flow dynamics in porous media such as soil is typically achieved by solving an agro-hydrological model, the most important of which being the Richards equation. To overcome the computational challenges associated with solving this highly nonlinear partial differential equation (PDE), in this paper, we present a novel solution algorithm, which we name as the DRW (Data-driven global Random Walk) algorithm, that holistically integrates adaptive L-scheme, neural networks, and global random walk in a finite volume discretization framework. We thoroughly discuss the need and benefits of introducing these components to achieve synergistic improvements in solution accuracy and numerical stability. Furthermore, we show that the DRW algorithm can accurately solve the mixed-form n-dimensional Richards equation with guaranteed convergence under reasonable assumptions. Through several illustrative examples, we demonstrate that the DRW algorithm not only achieves superior accuracy, but also better preserves the underlying physics and mass conservation of the Richards equation compared to state-of-the-art solution algorithms and commercial solver. Furthermore, the data-driven feature of our DRW algorithm makes it amenable for integrating with soil sensing technologies for root-zone soil moisture monitoring leveraging real-time soil sensor measurements. Overall, the proposed data-driven numerical method is expected to be a generalizable framework for modeling a wide range of applications, including fluid transport in fibrous porous materials, liquid extraction from saturated granular materials, water and hydrocarbon flow in petroleum reservoirs, etc.

   @misc{song2023datafacilitated,
     title = {A Novel Numerical Method for Agro-Hydrological Modeling of Water Infiltration in Soil},
     author = {Song, Zeyuan and Jiang, Zheyu},
     year = {2023},
   }